1 BST

BST (Binary Search Tree) 二叉搜索树, 在key 恰好有序的时候，会退化成链表。

Conclusion

  • BST 的查询复杂度取决于树的高度, 树的高度即最大比较次数。
  • 一棵具有 N 个 node 的 BST 树高(height)取值范围为：logN ≤ height ≤ N

因此，BST越平衡，在树中查找的时间就越短，连带地插入，删除也会变得效率更高。

红黑树的特征

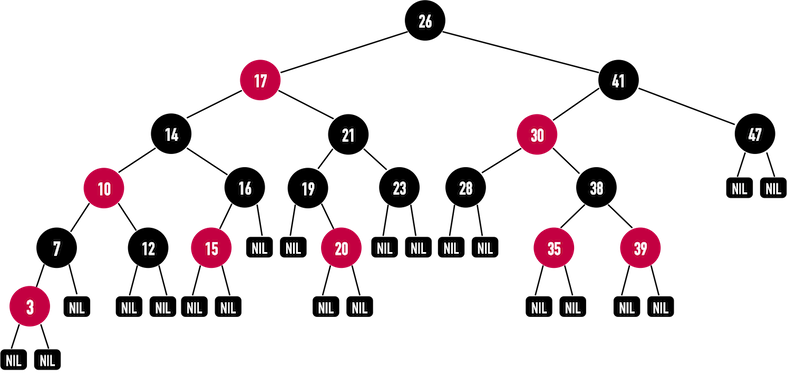
红黑树（RBT）是节点涂了「颜色」的二分搜索树（BST），借助颜色控制，能够保证在 RBT 中，最长路径(path)不会超过最短路径的2倍（若最短的路径是5，最长的路径至多只能是10），如此，RBT便能够近似地视为平衡，如下图：

rb-tree

上图：最短的path为3（最右路径：26-41-47），其余路径最长只能是6（最左路径：26-17-14-10-7-3）。若遮住NIL和颜色，此即为BST。

有原本在BST中指向NULL的指针，在RBT中，全部指向了NIL。

什么是NIL？NIL是永远为黑色，并且实际占有内存的节点，因为占有内存，因此能够以 node->color 的方式获得某个节点的颜色（若使用NULL则没有办法），这样的设计将在后续介绍如何于RBT中Insert（新增资料）与Delete（删除资料）时派上用场。

接下来看RBT的五项特征：

1 RBT 中的每一个节点不是黑色就是红色。
2 root 一定是黑色。
3 每一个叶子节点 leaf node（也就是NIL）一定是黑色。
4 如果某个 node 是红色，那么其两个 child 必定是黑色，不能有两个红色 node 相连，如上图中的node(17)、node(30)。
若某个 node 为黑色，其 child 的颜色没有限制，如上图中的 node(38)、node(26)、node(21)。
5 站在任何一个 node 上，所有从该 node 走到其任意 descendant leaf 的path上的黑色 node 数必定相同。

  • 如上图，站在node（14）上，所有从node（14）走向其descendant leaves（也就是NIL）的路径上之黑色node数必为3：
  • path1:14(b)-10(r)-7(b)-3(r)-NIL(b)；
  • path2:14(b)-10(r)-7(b)-NIL(b)；
  • path3:14(b)-10(r)-12(b)-NIL(b)；
  • path4:14(b)-16(b)-15(r)-NIL(b)；
  • path5:14(b)-16(b)-NIL(b)；

其中，第 4 点和 第 5 点比较难理解:
第4点：红色节点的孩子只能为黑色节点，黑色节点的孩子则没有这个约束（但是有第5点约束）。
第5点：站在任何一个节点上，从该 node 到所有叶子节点路径上的黑色节点数 必定相同。

程序编码

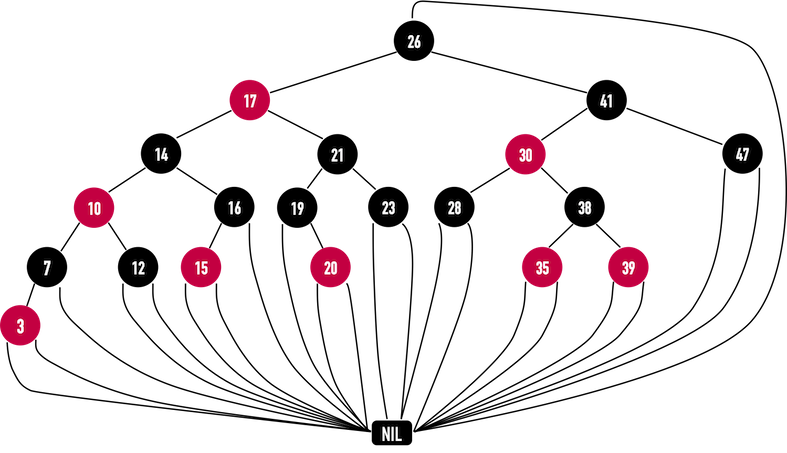
实际的程序实现上，会把所有NIL视为同一个NIL，并把根的父母指向NIL，以节省存储空间。

rb-tree-imp

class TreeNode与class RBT之资料成员（数据成员）程序范例如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

// C++ code
#include <iostream>
#include <string>

class RBT;
class TreeNode{
private:
    TreeNode *leftchild;
    TreeNode *rightchild;
    TreeNode *parent;
    std::string element;
    int key;
    int color;         // 0: Red, 1: Black; using type:bool is ok
    friend RBT;
    ...
}
class RBT{
private:
    TreeNode *root;
    TreeNode *neel;    // 为NIL, 常被称为哨兵(sentinel)
    ...
}

（为了避开某些IDE将NIL设置成保留关键字（保留关键字，例如template，while，struct等等），因此使用neel。）
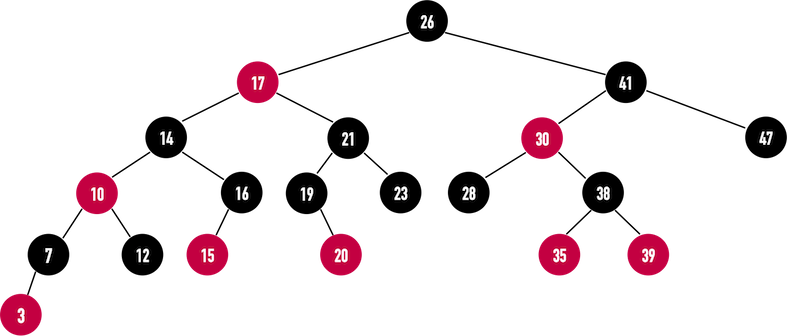
为求画面简洁，往后的篇幅里将把RBT示意图中的NIL隐藏起来，只显示RBT中的内部节点，就像下图，不过心里要记得，RBT无时无刻都被NIL充满着。

rb-tree-simple

以上便是RBT之初探，最重要的事实：就时间复杂度而言，RBT能够被视为平衡的BST，所有操作皆能在时间复杂度为O（logN）内完成。

在接下来，将依序介绍Rotation，Insert与Delete。

Problem

为什么map 不使用 avl-tree, 而使用rb-tree?

avl-tree 是高度平衡的 BST, 查询效率为O(logN), avl-tree 所有节点的左右子树高度差不超过1。 当有大量插入(or 删除)需求的时候，为了维持高度平衡，需要大量节点旋转调整，成本比较高。

在map/set等内核数据结构中，大量使用的是rb-tree， rb-tree 查询复杂度也是 O(logN)。 rb-tree的平衡性要比 avl-tree 差一些，但是这也带来了好处：当有大量插入(or 删除)需求的时候，节点调整的代价相对较低。 所以这也是一种 trade-off。